안녕하세요. 여러분!!
이번 포스팅에서는 삼각형 변 길이를 사인과 코사인으로 나타내는 것을 포스팅하려고 합니다.
일단, 사인과 코사인에 대해 저번 포스팅에서 쉽게 이해하고 익혀두는 법을 포스팅했죠.
https://twentyforseven.tistory.com/entry/사인-코사인-탄젠트-쉽게-이해해서-익혀두자-삼각함수-기본-개념
사인, 코사인, 탄젠트 쉽게 이해해서 익혀두자. (삼각함수 기본 개념)
특수각, 특수삼각비에 이어 포스팅합니다!! 집중입니다!!! 어렵지 않으니까 자신감을 갖고 시작해봅시다. https://twentyforseven.tistory.com/entry/특수각-특수삼각비-삼각-함수에서-꼭-알아둬야-할-기본-
twentyforseven.tistory.com
못 보신 분들은 위 링크를 참고하시면 됩니다.
복습 겸, 다시 해보겠습니다.
사인은
' 주어진 각도에서 출발해서 직각이 아닌 다른 각으로 돌아서 직각으로 도착한다. '
코사인은
' 주어진 각과 직각이 아닌 다른 각에서 출발해서 주어진 각으로 돌아 직각으로 도착한다. '
라고 했습니다.
잊지 않으셨죠? 복습은 정말 중요합니다.
이해를 꼭 하고 암기해야 한다는 점 꼭 잊지 마시길 바랄게요.
자, 그럼 본론으로 들어가 보겠습니다.
직각삼각형에서 한 변의 길이가 주어진다면 다른 두 변의 길이를 사인과 코사인으로 나타낼 수 있습니다.

위 삼각형은 저희가 너무나 잘 알고 있는 30도와 60도로 이루어진 직감삼각형입니다.
지금부터 집중입니다!!!!! 연습장 꺼내서 따라오세요.
사인 60도 = 2 분의 루트 3
양변에 2를 곱해주면?
루트 3 = 2 곱하기 사인 60도가 됩니다.
코사인 60도는 = 2분의 1
양변에 2를 곱해주면?
1 = 2 곱하기 코사인 60도가 됩니다.
느낌이 오시지 않나요?
2를 제외한 나머지 두 변의 길이, 1과 루트 3은 각각 2*cos60도, 2*sin60도로 표현이 됩니다!!
( * 는 곱하기 표현입니다.)
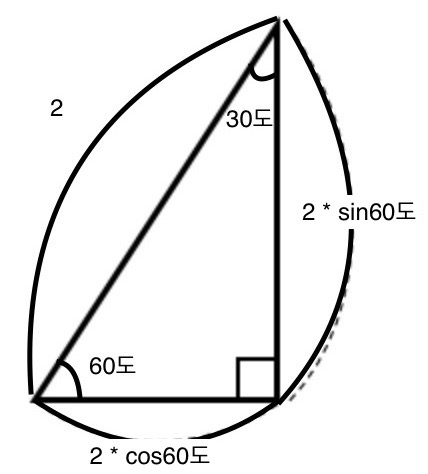
위 사진과 같이 나머지 두 변을 사인과 코사인으로 나타낼 수 있습니다.
어렵지 않죠? 정말 쉬운 과정이었습니다.
예시로 보기 쉬운 특수각으로 이뤄진 직각삼각형으로 들었지만,
꼭 특수각으로 이뤄진 삼각형이 아니더라도 다른 삼각형에서도 적용할 수 있습니다.
결론을 말씀드리자면, 이렇게 꼭 말로 외쳐보세요.
' 삼각형에서 한 변의 길이가 주어진다면 나머지 두 변의 길이를 사인과 코사인 값으로 나타낼 수 있다. '
스스로 말로 표현해보거나 친구들에게 직접 설명을 해준다면 더 기억에 오래 남을 겁니다.
외울 것도 없지 않나요? 너무나도 당연하고 여러분들은 충분히 할 수 있는 실력을 갖고 있는 분들이란 걸 믿어 의심치 않습니다.

( 편집할 때 삼각형이 좀 잘렸네요 ㅜㅜ 이해 부탁드립니다. )
' 삼각형에서 한 변의 길이가 주어진다면 나머지 두 변의 길이를 사인과 코사인 값으로 나타낼 수 있다. '
이 문장을 스스로 설명해 보면서 위 사진을 보고 값을 구해보세요.
길이가 주어진 변 선분 AB = 3
선분 AC = 3*cos세타
선분 BC = 3*sin세타
( 세타는 각도를 나타내는 말입니다. )
이상으로 삼각형에서 한 변의 길이가 주어질 때 나머지 두 변을 사인과 코사인으로 나타내는 과정을 거쳐봤습니다.
삼각함수 단원 과정에서 정말 중요한 과정이기 때문에,
눈으로만 보는 것이 아니라 꼭 연습장을 꺼내서 복습하고 익히셔서
응용문제를 풀어나갈 때 유용한 도구로 만드시길 바랍니다!
다음 포스팅으로 돌아오겠습니다.
수험생 여러분들 항상 파이팅입니다!!!!
위에 걸어둔 링크에 특수각도에 따른 사인, 코사인, 탄젠트 값을 정리해 놨으니까
꼭 이해하고 암기하기!

'수학 개념' 카테고리의 다른 글
| 함수 그래프 대칭이동 쉽게 이해하고 한번에 끝내자 ( 함수 그래프 응용 ) (0) | 2023.04.07 |
|---|---|
| 탄젠트 값은 무엇을 의미할까? ( 삼각함수 기본개념 ) (1) | 2023.04.05 |
| 원의 특징 중심각과 원주각 ( 삼각함수 기본개념 ) (0) | 2023.04.01 |
| 사인, 코사인, 탄젠트 쉽게 이해해서 익혀두자. (삼각함수 기본 개념) (0) | 2023.03.29 |
| 특수각, 특수삼각비 ( 삼각 함수에서 꼭 알아둬야 할 기본 개념 ) (0) | 2023.03.28 |



