연립부등식 , 식으로 푸는 풀이법을 알기 전에 그래프 모양으로 해석하는 풀이법을 무조건 알아야 한다. ( 함수 그래프 이해하기 )
안녕하세요.
연립 부등식에서 식으로 푸는 방법을 아는 학생분들은 많습니다.
하지만, 정작 그래프 모양으로 해석해서 설명할 수 있는 학생분들은 매우 드물더라구요.

이번 포스팅에서는 함수의 대소관계를 통해서 그래프를 그려보려고 합니다.
이해하고 나면 엄청난 힘을 발휘할 수 있는 개념 부분이니까 꼭 집중해서 익히시길 바랍니다.
함수의 대소관계를 쉽게 풀어서 말해보자면,
함숫값의 크기를 비교한다는 소리입니다. 함숫값은 곧 y 값이란 소리죠.
그럼 바로 시작해 보도록 하겠습니다.
이차함수의 연립 부등식으로 설명해 보겠습니다.
이차함수의 그래프 모양은 두 가지죠. 양수의 그래프 모양. 음수의 그래프 모양.
양수 그래프는 아래로 볼록한 모양이고 음수 그래프는 위로 볼록한 모양입니다.
두 함수 y = x^2 - 1 과 y = -x^2 + 1 의 그래프를 봐보도록 하겠습니다.

위 사진을 이해를 하셔야 합니다. 천천히 해석해 봅시다.
1번과 2번은 f(x)의 함숫값이 g(x)의 함숫값보다 큰 영역입니다.
3번은 g(x)의 함숫값이 f(x)의 함숫값보다 큰 영역입니다.
4번은 f(x)와 g(x)가 만나는 곳이므로 함숫값이 같은 영역입니다.
한 그래프가 다른 그래프보다 위에 있으면 함숫값이 크고,
한 그래프가 다른 그래프보다 아래 있으면 함숫값이 작다는 말입니다.
두 그래프가 겹치는 곳은 함숫값이 같다는 말입니다.
이해하셨나요? 꼭 이해하셔야 합니다.
저 그림을 토대로 다시 함수를 그려보겠습니다.
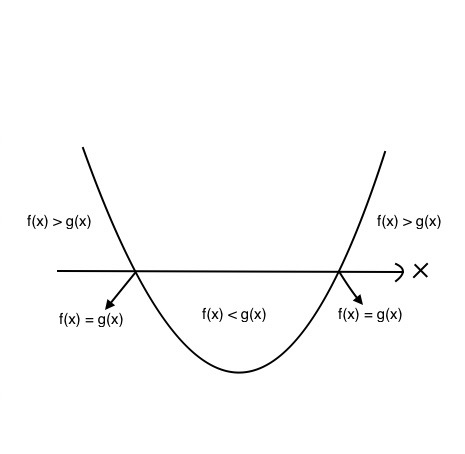
이렇게 그려집니다. 여러분 이 그림을 꼭 이해하셔야 합니다.
다음 포스팅에서 연립부등식을 식으로 푸는 풀이법으로 설명을 드리겠습니다.
여러분, 위 두 그림을 보고 꼭 이해해 보시길 바랍니다.
연립 부등식을 식으로 간단하게 풀 수 있기는 하지만,
쉬운 문제에서는 유용하겠지만,
활용 문제로 들어가게 된다면 위 과정으로 해결해나가야 하는 중요한 재료인 부분이 되기 때문에
식으로만 푸는 풀이법이 아닌 함수 그래프로 해석할 수 있는 능력을 길러야 합니다.
다음 포스팅에서 뵙도록 하겠습니다.
항상 파이팅입니다!!!

'수학 개념' 카테고리의 다른 글
| 절댓값 함수 그래프 모양, 개념만 안다면 충분히 쉽게 그릴 수 있다. (0) | 2023.04.18 |
|---|---|
| 절댓값에 대해 알아보자 (2) | 2023.04.17 |
| 우함수 기함수 이렇게 알아두자 ( 식을 외우지 말고, 이해해보자 ) (0) | 2023.04.15 |
| 탄젠트 함수 그래프 특징 ( 삼각함수 그래프 ) (0) | 2023.04.14 |
| 코사인 함수 그래프 특징 ( 삼각함수 그래프 ) (0) | 2023.04.13 |



