안녕하세요!!
이번 포스팅에서는 피타고라스 정리와
피타고라스 정리를 적용하여 점과 점 사이의 거리를 구해보려고 합니다.
시작해 봅시다.
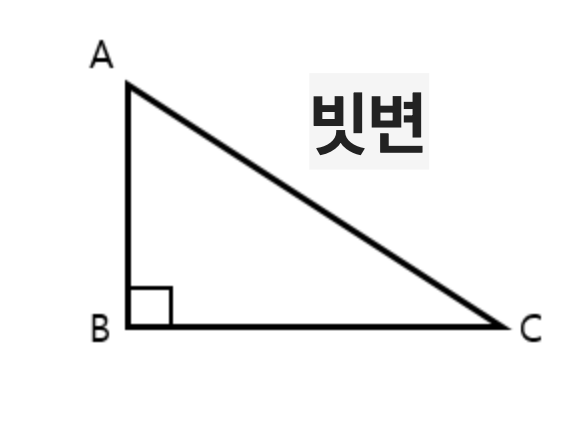
위와 같이 직각삼각형이 보이시죠.
직각 삼각형에서 선분 AC를 빗변이라고 부릅니다.
밑변과 높이는 어딨 냐고요? 밑변과 높이는 상대적이 개념이기 때문에 존재하지 않습니다.
따라서 빗변이라는 절대적인 개념 밖에 없습니다.
그렇기에 빗변을 제외한 나머지 두 변이라고 부릅니다.

피타고라스의 정리는 다음과 같습니다.
' 빗변 길이의 제곱은 나머지 두 변 길이를 각각 제곱하여 합한 값이다. '
위 직각삼각형 기준으로 공식을 적어볼까요?
(선분 AC)^2 = (선분 AB)^2 + (선분 BC)^2
( ^ 이라는 기호는 거듭제곱 표현입니다.)
이렇게 표현할 수 있습니다.
공식보다는 말로 설명할 수 있어야 더 기억에 오래 남습니다.
아주 잘 활용되는 개념이니까 꼭 알아두시길 바랍니다.
고1 수학 과정에서 점과 점 사이의 거리를 구하는 단원이 나오게 되는데
피타고라스 정리가 적용되어 있다는 점 알고 계신가요?
점과 점 사이 거리 공식이 중요한 것이 아니라 이 공식이 어떻게 생겼는지 과정을 알아야 합니다.
합리화 과정을 거치고 이해한 후 암기를 해도 좋습니다.

좌표평면 위 두 점 (1,1)과 (5,3) 이 있습니다.
두 점을 이은 선분을 빗변이라고 생각해 보시고 직각삼각형을 만들어볼까요?

이렇게 되겠죠?
각 두 점 x좌표의 차는 4, 두 점 y좌표의 차는 2가 되고 이 값들이 어디 위치에 있는지 보이시죠.
두 점 사이거리가 빗변이 되고 두 점 x좌표끼리의 뺀 값, y좌표끼리 뺀 값이 빗변을 제외한 나머지 두 변이 되는 것입니다.
그렇다면 피타고라스 정리를 이용한다면 두 점 사이거리를 구할 수 있는 것입니다.
빗변의 제곱 = (x좌표끼리 뺀 값)^2 + (y좌표끼리 뺀 값)^2
빗변의 제곱 = 16 + 4 = 20
따라서 빗변 = 루트 20 = 2 루트 5.
구하고자 하는 두 점 사이의 거리는 2 루트 5 입니다.
이렇게 피타고라스 정리를 이용하여 두 점 사이 거리를 어떻게 구했는지 합리화 과정을 거쳐봤습니다.
두 점 사이 거리 공식은 써두고 싶지가 않네요 ㅎㅎ
공식만 보고 외우는 학생들이 많기 때문에 검색해 보면 두 점 사이 거리 공식을 볼 수 있을 겁니다.
복잡해 보이는 공식이지만 위 과정을 거쳐 해석할 줄 아셔야 사고력이 길러집니다.
' 두 점 사이 거리는 x좌표끼리 빼고 제곱한 값과 y표끼리 빼고 제곱한 값을 더한 후 루트를 씌운 것! '.
이렇게 해석이 가능해야 합니다.
꼭 합리화 과정을 거친 후 이해하고 외우시길 바랍니다!!!! 꼭이요.
다음 포스팅으로 돌아오겠습니다.

'수학 개념' 카테고리의 다른 글
| 사인, 코사인, 탄젠트 쉽게 이해해서 익혀두자. (삼각함수 기본 개념) (0) | 2023.03.29 |
|---|---|
| 특수각, 특수삼각비 ( 삼각 함수에서 꼭 알아둬야 할 기본 개념 ) (0) | 2023.03.28 |
| 호도법 (각도를 파이로 나타내보자) (0) | 2023.03.26 |
| 일차함수끼리 직각을 이룬다 (기울기 곱을 알아보자) (0) | 2023.03.24 |
| 원의 방정식 (원은 왜 함수가 아닐까?) 외우지 말고 이해해보자 (0) | 2023.03.23 |



